问题:集数据--做分类,找要因--抓重点--追原因--控制异常--改善不良
我们先看下新旧七大手法的对比:
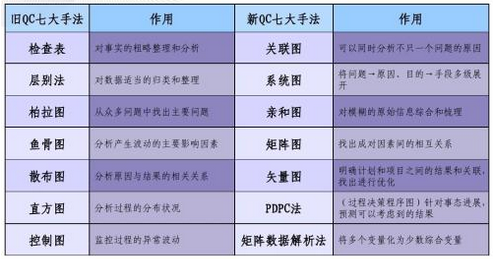
旧qc七大手法(主要用于品质改善提高)
1.检查集数据
2.层别作解析
3.柏拉抓重点
4.因果追原因
5.散布看相关
6.直方显分布
7.管制找异常
1.检查表(又称我们的数据库,大数据)
定义:所谓数据,就是根据测量所得到的数值和资料等事实,数据=事实。
收集重点:
1.收集正确的数据。
2.避免主观的判断。
3.要把握事实真相。
数据的种类:
1. 定量数据计量值:如长度、时间、重量等连续性数据。
2.计数值:如缺点数、不良品数、人数等非连续性数据。
3. 定性数据如衣服的美感等以优先顺序、等级为依据的数据。
用途说明:1.日常管理。2.收集数据。3.改善管理。
制作步骤:1.决定所要收集的数据及希望把握的项目。2.决定查检表的格式。3.决定记录形式。4.决定收集数据的方法。
使用要诀:
查检收集完成的数据应马上使用。数据是否集中在某些项目或某些时段?是否因时间的经过而产生变化?周期性变化的特殊情形也要特别注意。
如有异常,应马上追究原因,并采取必要的措施。迅速判断,即刻行动。
是否随着改善而有变化?适当保留过去、现在及未来的记录,以便日后比较。可利用柏拉图加以整理,以便更进一步掌握问题的重心。
2.层别法:
定义:对观察到的现象或所收集到的数据,按照它们共同的特征加以分类、统计的一种分析方法。是容易观察,有效掌握事实的最有效、最简单的方法。
用途说明:1.发现问题,界定问题。2.发掘问题的要因。3.验证要因产生的影响。
层别的对象和项目:1.有关人的层别。2.机械设备的层别。3.作业方法、条件的层别。4.时间的层别。5.原材料零件别。6.测量检查的层别。7.环境天候的层别。8.制品的层别。
使用步骤:
确定目的,掌握影响问题的因素及范围。决定层别项目、收集使用表单。层别观察事实并记录、分类与绘制应有的图表。寻求差异点,找寻真因所在。得出结论。
实例:白班和夜班也就是a班和b班的不良数分析,利用层别法如下:全部+a班+b班

从以上可以看出A班的不良数较多。
且从上图的层别中发现不管是A班还是B班的0-5阶段不良最多。
3.柏拉图:
定义:又称重点管理图,根据所收集的数据,以不同区分标准加以整理、分类,计算出各分类项目所占的比例而按照大小顺序排列,再加上累积值的图形。
制作步骤:决定不良的分类项目。决定数据收集期间,并且按照分类项目收集数据。记入图表纸。
计算累计比率。标记代表意义。记上累计值,并用线连接。计入柏拉图的主题及相关资料。
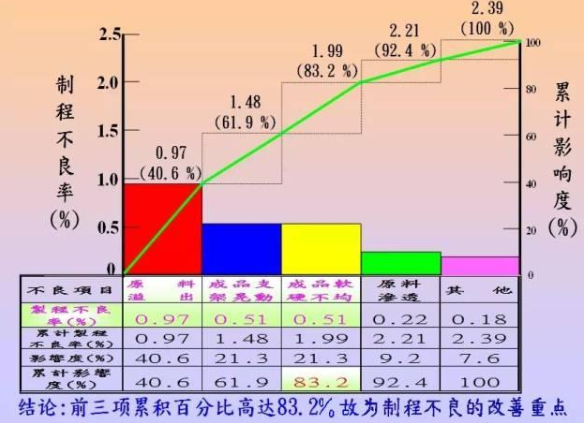
柏拉图能够从一些数据中主观的给我们一些改善的结果,可以结合查检表一起应用:

4.因果图(又称特性要因图、石川图、鱼骨图)
定义:当一个问题的特性(结果)受到一些要因(原因)影响时,将这些要因加以整理,
成为有相互关系且有条理的图形,这个图形就称为特性要因图,又叫鱼骨图(Fish-Bone Diagram)。
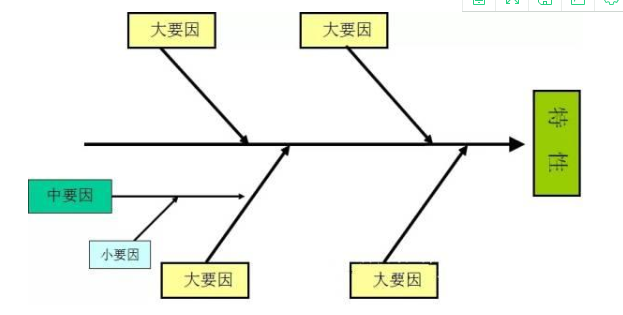
用途说明:1.整理问题。2.追查真正的原因。3.寻找对策。
制作步骤:1. 决定问题或品质的特性——特性的选择不能使用看起来很抽象或含混不清的主题。
2. 决定大要因 ——须是简单的完整句,且具有某些程度或是方向性。
3. 决定中小要因。
4. 决定影响问题点的主要原因。
5. 填上制作目的、日期及制作者等资料。
应注意事项:1.脑力激荡。2.以事实为依据。3.无因果关系者,予以剔除,不予分类。4.多加利用过去收集的资料。
5.重点放在解决问题上,并依结果提出对策,
依5W2H原则执行。
WHY——为什么?为什么要这么做?理由何在?原因是什么?
WHAT——是什么?目的是什么?做什么工作?
WHERE——何处?在哪里做?从哪里入手?
WHEN——何时?什么时间完成?什么时机最适宜?
WHO——谁?由谁来承担?谁来完成?谁负责?
HOW ——怎么做?如何提高效率?如何实施?方法怎样?
HOW MUCH——多少?做到什么程度?数量如何?质量水平如何?费用产出如何?
6.依据特性别,分别制作不同的特性要因图。
7. a.大要因通常代表是一个具体方向。b.中要因通常代表的是一个概念、想法。 c.小要因通常代表的是具体事件。
8.至少要有4根大骨、3根中骨及2根小骨,且这些要因都不能重复。
比如下面的一个实例很好的解析了因果图:

5.散布图:
定义:把互相有关联的对应数据,在方格纸上以纵轴表示结果,以横轴表示原因;然后用点表示出分布形态,根据分布的形态来判断对应数据之间的相互关系。
用途说明:1.检定两变数间的相关性。2.从特性要求寻找最适要因。3.从要因预估特性水准。

目的:
知道两组数据(或原因与结果)之间是否有相关及相关程度。依据各种可能影响原因层别绘制散布图,可找出最适的要因。检视是否为不相关。
制作步骤:
收集相对应数据,至少30组以上,并且整理写到数据表上。找出数据之中的最大值和最小值。画出纵轴与横轴刻度,计算组距。将各组对数据标示在座标上。记录必要事项。
例子:

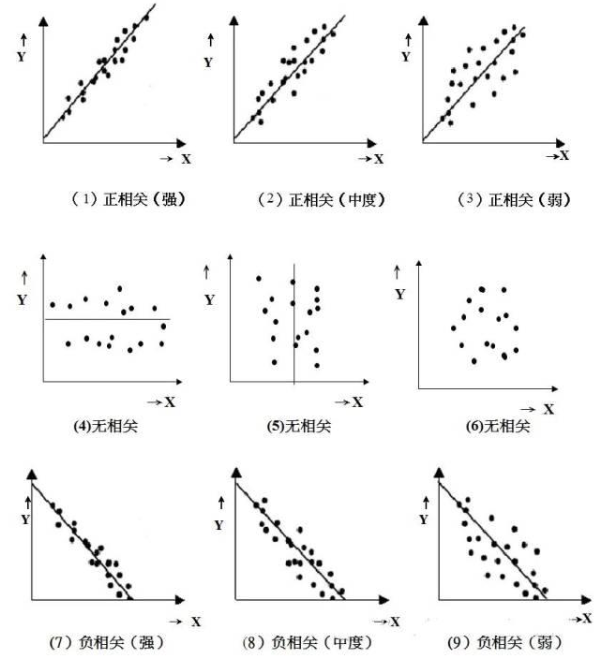
6.直方图:
定义:将所收集的数据、特性值或结果值,在横轴上适当地区分成几个相等区间,并将各区间内测定值所出现的次数累加起来,用柱形画出的图形。
使用目的:1.测知制程能力。2.测知数据的真伪。3.测知分配型态。4.计算产品不良率。
5.调查是否混入两个以上的不同群体。6.藉以制定规格界限。
7.规格与标准值比较。8.设计管制界限是否可用于制程管制。9.求分配的平均值与标准差。
例子:比如我们需要了解一批西瓜的重量:
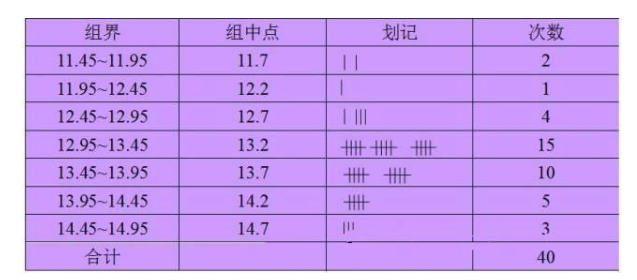

其中n为总数,x为中间值,一般做此类表时:横轴为计算间距,比如找出最大值和最小值,然后划分几组数据,然后再绘制直方图。
7.管制图:
定义:将实际的质量特性,与根据过去经验所建立的制程能力的管制界限比较,按时间的先后或制品全体号码的次序,以判别产品质量是否安定的一种图形。
管制图的功用:1. 任何生产过程中,影响质量差异的原因不外是机遇原因与非机遇原因两种。——机遇原因:不可避免的原因——非机遇原因:可避免的原因
2. 防止非机遇原因再度发生,维持制程稳定。
依数据的性质分类:1. 计量值管制图——用来测量长度、重量、面积、温度、时间等计量值的管制图。 2. 计数值管制图——用来计算不良数、缺点数等计数值的管制图。
依用途来分类:1. 解析用管制图——为了调查制程是否处于统计管制的状态。 2. 管制用管制图——为了保持完善管理的制程。
管制图的分析:1. 管制状态下的管制图
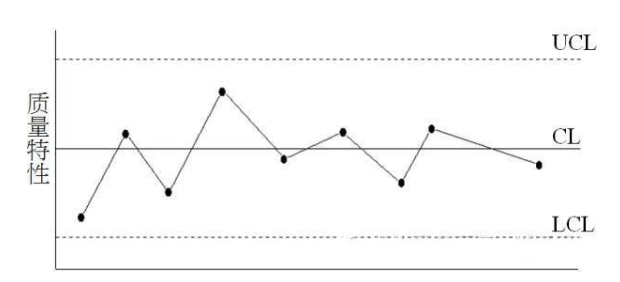
结束语总结:在实际应用中要灵活使用以上工具,并且以上工具都可以组合使用,比如检查表就是所有数据的来源,没有检查表一切等于0
拓展: qc七大手法的详细应用,可以参照以下文献:
https://baijiahao.baidu.com/s?id=1664286154000164032&wfr=spider&for=pc
转载请注明:首页 > 学习笔记 > 随笔记录 » qc七大手法分析问题基本解析


